
문제
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
입력
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다.
다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다.
이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다.
최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.
출력
첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.

문제 해결
직전 학기인 2학년 2학기 때 수강한 자료구조 과목에서 배웠던 최소 스패닝 트리(최소 신장 트리) 문제다. 학점 관리를 위해 나름 열심히 했던 덕분인지 내 머릿속에 배웠던 내용들의 온기가 아직 남아있었다.
신장 트리 : 신장 트리는 그래프 G의 최소 부분 그래프(minimal subgraph) G'로서 V(G') = V(G)이고 G'은 연결되어 있다. G의 정점의 개수를 n이라 했을 때, 신장 트리는 n-1개의 간선을 갖는다. 이를 위해 신장 트리는 몇 가지 조건을 갖는데 이는 다음과 같다.
신장 트리의 제한 조건 : 그래프 내의 간선들만을 사용, 정확하게 n-1개의 간선만을 사용, 사이클을 생성하는 간선은 사용 금지.
선택된 간선이 사이클을 형성하는지 알아내는 방법은 여러 가지가 있겠지만 나는 disjoint set의 weighted union을 이용했다. parent[i]는 i의 부모를 가리키며, i가 루트인 경우 트리에 속한 노드의 개수를 음수로 저장한다. 단절된 두 트리 t2를 t1에 합치는 방법은 parent[t1] = parent[t1] + parent[t2]로, parent[t2] = t1으로 바꾼다.

위의 그림에서 (c)의 두 트리는 parent[i]에 다음과 같이 나타나지만
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| parent[i] | -4 | 0 | 0 | 2 | -4 | 4 | 4 | 6 |
(d)에서 두 트리를 합친 결과는 다음과 같다.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| parent[i] | -8 | 0 | 0 | 2 | 0 | 4 | 4 | 6 |
최소 비용 신장 트리 : 신장 트리 중에 최저의 비용을 갖는 신장 트리.
최소 신장 트리 문제를 해결하기 위해서 크게 kruskal, prim과 sollin 세 가지 방법을 사용할 수 있지만, 이 방법들은 모두 그리디 알고리즘이 베이스라는 점을 명심하자.
① kruskal 알고리즘 :
− 한번에 하나씩 T에 간선을 추가해가면서 최소 신장 트리 T를 구축
− T에 포함될 간선을 비용의 크기순으로 선택
− 이미 T에 포함된 간선들과 사이클을 형성하지 않는 간선만을 T에 추가
− G는 연결되어 있고 n > 0개의 정점을 가지므로 정확하게 n-1개의 간선만이 T에 포함됨.

kruskal 알고리즘을 이용한 최소 신장 트리 문제의 해결 방법은 모든 간선들 중 가장 작은 간선들부터 고르되, 이미 선택된 정점들끼리의 간선은 사이클을 형성하므로 선택하지 않는다.
이를 위해서는 priority_queue에 양쪽 정점과 가중치의 정보를 저장한 모든 간선들을 넣고, 작은 가중치의 간선부터 선택해나가면 된다.
우선순위 큐에서 작은 가중치 값으로 선택된 간선의 두 정점이 같은 최소 신장 트리에 존재할 경우 사이클을 형성하므로 선택하지 않고, 다른 트리에 존재할 경우 해당 간선을 선택하고 하나의 트리로 합친다.
// kruskal algorithm
#include <iostream>
#include <queue>
using namespace std;
struct Edge {
int v1, v2, weight;
Edge(int a, int b, int c) :v1(a), v2(b), weight(c) {}
};
class Compare {
public:
bool operator()(Edge e1, Edge e2) { return e1.weight > e2.weight; }
};
int ans, V, E, parent[10001];
priority_queue<Edge, vector<Edge>, Compare> pq;
void WeightedUnion(int i, int j) {
int tmp = parent[i] + parent[j];
if (parent[i] > parent[j]) {
parent[i] = j;
parent[j] = tmp;
}
else {
parent[j] = i;
parent[i] = tmp;
}
}
int Find(int i) { while (parent[i] >= 0) i = parent[i]; return i; }
void kruskal() {
int nedges = 0;
while ((nedges < V - 1) && !pq.empty()) {
Edge e = pq.top();
pq.pop();
int x = Find(e.v1);
int y = Find(e.v2);
if (x != y) {
WeightedUnion(x, y);
nedges++;
ans += e.weight;
}
}
}
void ReadEdges4kruskal() {
int a, b, c;
while (E--) {
scanf("%d %d %d", &a, &b, &c);
pq.push(Edge(a, b, c));
}
}
int main() {
fill(parent, parent + 10001, -1);
cin >> V >> E;
ReadEdges4kruskal();
kruskal();
cout << ans;
}
② prim 알고리즘 :
− 결과적으로는 모든 정점이 포함되어야 하므로 임의로 시작 정점을 선택 후 최소 신장 트리 T에 추가하고 해당 정점이 포함된 모든 간선을 우선순위 큐에 추가
− 최소 신장 트리 T에 속한 정점들(u) 중 가장 작은 가중치를 가진 간선 선택
− 선택된 간선 (u,v)가 사이클을 만들지 않으면(반대쪽 정점이 트리에 속해 있지 않음) T에 추가하고 반대쪽 정점이 포함된 모든 간선 (v, x)을 우선순위 큐에 추가.
− 선택된 간선의 개수가 n-1개가 될 때까지 반복
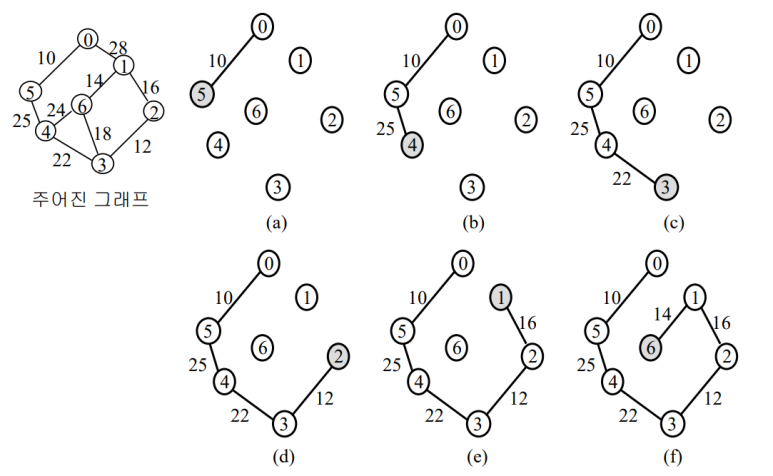
prim 알고리즘은 하나의 최소 신장 트리 T에 대하여, 인접한 정점들 중 사이클을 만들지 않으며 가장 작은 간선을 포함하는 정점을 추가한다고 생각하면 된다.
한 정점이 추가될 때마다 해당 정점이 포함된 모든 간선들을 우선순위 큐에 넘겨야되므로, 각 정점에 해당 간선들을 저장해야 한다.
// prim algorithm
#include <iostream>
#include <queue>
using namespace std;
struct Edge {
int v1, v2, weight;
Edge(int a, int b, int c) :v1(a), v2(b), weight(c) {}
};
class Compare {
public:
bool operator()(Edge e1, Edge e2) { return e1.weight > e2.weight; }
};
int ans, V, E, parent[10001];
priority_queue<Edge, vector<Edge>, Compare> pq;
queue<Edge>* q;
void WeightedUnion(int i, int j) {
int tmp = parent[i] + parent[j];
if (parent[i] > parent[j]) {
parent[i] = j;
parent[j] = tmp;
}
else {
parent[j] = i;
parent[i] = tmp;
}
}
int Find(int i) { while (parent[i] >= 0) i = parent[i]; return i; }
void MoveInto(int v) { // 우선순위 큐에 간선들을 넘겨주는 함수
while (!q[v].empty()) {
pq.push(q[v].front());
q[v].pop();
}
}
void prim() {
int nedges = 0;
while (nedges < V - 1) {
Edge e = pq.top();
pq.pop();
int x = Find(e.v1);
int y = Find(e.v2);
if (x != y) {
WeightedUnion(x, y);
nedges++;
ans += e.weight;
MoveInto(x);
MoveInto(y);
}
}
}
void ReadEdges4prim() {
q = new queue<Edge>[V + 1]; // 정점마다 간선을 저장하기 위한 큐 배열
int a, b, c;
while (E--) {
scanf("%d %d %d", &a, &b, &c);
q[a].push(Edge(a, b, c));
q[b].push(Edge(a, b, c));
}
MoveInto(1);
}
int main() {
fill(parent, parent + 10001, -1);
cin >> V >> E;
ReadEdges4prim();
prim();
cout << ans;
}
③ sollin 알고리즘 :
− 각 단계에서 여러 개의 간선을 선택
− 각 단계에서는 포리스트에 있는 각 트리에 대해 하나의 간선을 선택
− 이 간선은 오직 하나의 정점만 그 트리에 속한 최소 비용 간선
− 선택된 간선은 구축 중인 신장 트리에 추가
− 오직 하나의 트리만이 존재하거나 더 이상 선택할 간선이 없을 때 종료

sollin 알고리즘은 모든 정점을 순회하며 각 정점의 최소 간선을 선택하여 그 간선이 사이클을 만들지 않으면 최소 신장 트리 T에 추가한다. 이 과정을 T의 간선의 개수가 n-1개가 될 때까지 반복한다.
위 그림에서 (a)는 정점 0부터 6까지 for문을 한 번 돌았을 때, (b)는 정점 0부터 6까지 for문을 다시 돌았을 때의 결과를 나타낸다.
각 정점마다 최소 비용의 간선을 선택해야 하므로 최소 우선순위 큐를 배열로 선언해야 한다. 그리고 선택된 정점을 T에 추가할 때 트리의 루트를 찾아, 루트에 넘겨주는 방식으로 작성했다.
// sollin algorithm
#include <iostream>
#include <queue>
using namespace std;
struct Edge {
int v1, v2, weight;
Edge(int a, int b, int c) :v1(a), v2(b), weight(c) {}
};
class Compare {
public:
bool operator()(Edge e1, Edge e2) { return e1.weight > e2.weight; }
};
int ans, V, E, parent[10001];
priority_queue<Edge, vector<Edge>, Compare>* spq;
queue<Edge>* q;
void WeightedUnion(int i, int j) {
int tmp = parent[i] + parent[j];
if (parent[i] > parent[j]) {
parent[i] = j;
parent[j] = tmp;
}
else {
parent[j] = i;
parent[i] = tmp;
}
}
int Find(int i) { while (parent[i] >= 0) i = parent[i]; return i; }
void MoveInto(int v, int root) {
while (!spq[v].empty()) {
spq[root].push(spq[v].top());
spq[v].pop();
}
}
void sollin() {
int nedges = 0;
while (nedges < V - 1) {
for (int i = 1; i <= V; i++) {
if (spq[i].empty()) continue;
Edge e = spq[i].top();
spq[i].pop();
int x = Find(e.v1);
int y = Find(e.v2);
if (x != y) {
WeightedUnion(x, y);
int root = Find(x);
ans += e.weight;
nedges++;
// 루트를 찾아 루트에 간선을 넘겨주는 작업
if (root == x) MoveInto(y, x);
else MoveInto(x, y);
}
}
}
}
void ReadEdges4sollin() {
spq = new priority_queue<Edge, vector<Edge>, Compare>[V + 1];
int a, b, c;
while (E--) {
scanf("%d %d %d", &a, &b, &c);
spq[a].push(Edge(a, b, c));
spq[b].push(Edge(a, b, c));
}
}
int main() {
fill(parent, parent + 10001, -1);
cin >> V >> E;
ReadEdges4sollin();
sollin();
cout << ans;
}'🎲 BOJ > 🥇' 카테고리의 다른 글
| [C++] 백준 5557 : 1학년 (0) | 2022.01.30 |
|---|---|
| [C++] 백준 1967 : 트리의 지름 (0) | 2022.01.30 |
| [C++] 백준 16236 : 아기 상어 (0) | 2022.01.27 |
| [C++] 백준 1963 : 소수 경로 (0) | 2022.01.27 |