문제

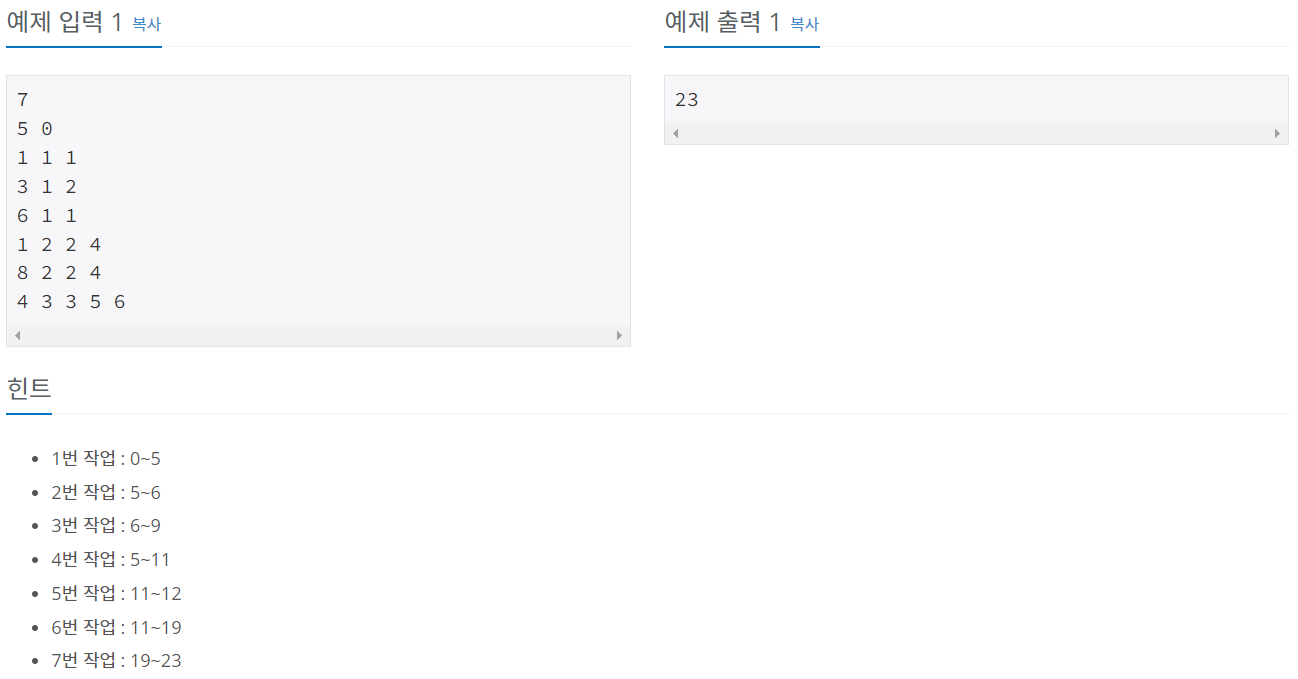
입력

출력

문제 해결
반례에 주의하자!!
R : 배열을 reverse하는 연산
D : 배열의 앞 원소를 pop하는 연산
R이 홀수개이면 마지막에 한 번만 reverse 연산을 하여 시간 복잡도를 개선한다. 대신 flag를 세워 앞에서 pop 할 건지, 뒤에서 pop 할 건지 체크해야 한다.
반례는 크게 세 가지가 있는데, 코드 블럭 내에 적혀있다.
코드
#include <iostream>
#include <list>
#include <algorithm>
using namespace std;
int t, n, z, res;
string s1, s2;
list<int> v;
/*
* 반례
* 1. 빈 배열에서 pop하는 경우 : error 출력
* 2. 빈 배열에서 R하는 경우 : [] 출력
* 3. 모든 함수 수행 후 빈 배열이 되는 경우 : [] 출력
*/
string input() {
int sum = 0;
cin >> s1 >> n >> s2;
for (int i = 1; i < s2.size(); i++) {
if (s2[i] >= '0' && s2[i] <= '9')
sum = 10 * sum + (int)(s2[i] - 48); // '0' = 48, '9' = 57
else if (s2[i] == ',' || s2[i] == ']') {
if (!n) break;
v.push_back(sum);
sum = 0;
}
}
return s1;
}
int solution(string s1) { // error : 0, not error : 1, empty array : 2
int s = s1.size();
int c = 1, cnt = 0;
bool flag = true; // true일 때는 pop_front, false일 때는 pop_back
for (int i = 0; i < s; i++) {
if (s1[i] == 'R') {
if (!v.size()) c = 2; // 2. 빈 배열에서 R하는 경우 : [] 출력
flag = !flag;
cnt++;
}
else if (s1[i] == 'D') {
if (!v.size()) return 0; // 1. 빈 배열에서 pop하는 경우 : error 출력
flag ? v.pop_front() : v.pop_back();
}
}
if (cnt % 2) reverse(v.begin(), v.end()); // R 연산이 홀수개인 경우 마지막에 한 번만 reverse
if (!v.size()) c = 2; // 3. 모든 함수 수행 후 빈 배열이 되는 경우 : [] 출력
return c;
}
int main() {
cin >> t;
while (t--) {
v.clear();
res = solution(input());
int z = v.size();
if (!res) {
cout << "error" << '\n';
continue;
}
else if (res == 2) {
cout << "[]" << '\n';
continue;
}
cout << '[';
list<int>::iterator iter = v.begin();
for (int i = 0; i < z - 1; i++) {
cout << *iter << ',';
iter++;
}
cout << *iter << ']' << '\n';
}
}'🎲 BOJ > 🥇' 카테고리의 다른 글
| [C++] 백준 4256 : 트리 (0) | 2023.08.06 |
|---|---|
| [C++] 백준 20922 : 겹치는 건 싫어 (0) | 2022.02.09 |
| [C++] 백준 1072 : 게임 (0) | 2022.02.08 |
| [C++] 백준 2533 : 사회망 서비스(SNS) (0) | 2022.02.07 |